1. 위상정렬이란?
위상정렬은 방향 그래프의 각 정점의 정해진 순서를 위배하지 않으면서,모든 정점을 나열하는 방법이다.
즉, 위상정렬이 필요한 대상은 순서가 정해져있는 작업이며, 순서가 뒤죽박죽 꼬여있는 node들을 주어진 순서에 따라 일렬로 정렬하는 데 유용하다.
몇 가지 예제를 보자.
(2) 백준 1766번 - 문제집
(3) Leetcode - Course Schedule
두 문제 모두 공통점이 있는데,
순서가 있는 노드 쌍(pair)이 입력으로 주어진다는 점,
그래프는 모두 사이클이 없는 방향 그래프(Directed Acyclic Graph)라는 점이다.
사이클이 존재하면 순서는 의미가 없다. 사이클이 존재하면 시작점도, 끝점도 의미가 없어지기 때문이다.
즉 위상정렬은 노드를 순서대로 일직선 상에 놓는 것이라 할 수 있다.
다만 위상정렬 시에는 결과가 2개 이상 나올 수도 있다.
1 -> 3 / 1- > 2 / 3 -> 4 / 2 -> 4
의 경우 , 1 - 3 - 2 - 4 또는 1 - 2 - 3 - 4 둘 다 답이 될 수 있기 때문이다.
만약 특정 문제가
“주어진 조건이 있을 때 조건을 고려하여 노드를 순서대로 정렬할 수 있는가?”를 묻는 문제라면,
위상정렬의 가능 유무를 따져보면 된다.
위상정렬을 하는 방법은 크게 두 가지가 있다.
2. 위상정렬 방법 1 - DFS
그래프에 순서가 있을 때,
DFS 결과의 맨 마지막 노드에서부터 분기를 거꾸로 따라가는 방법이 유효하다.
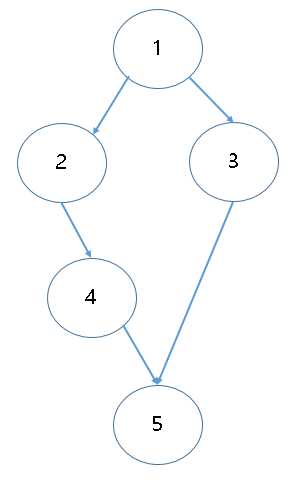
위 그래프에서,
정점 5는 4와 3이 만족되어야 하고,
4는 2가 만족되어야 하고,
2와 3은 각각 1이 만족되어야 한다.
DFS는 기본적으로 분기 를 따라가는 것이며, 조건을 만족하는 순서를 따라가는 것이므로,
DFS의 결과인 [ 5 - 4 - 2 - 3 - 1 ]을 역순으로 한 [ 1 - 3 - 2 - 4 - 5] 가 위상정렬의 결과가 된다( [1 - 2 - 4 - 3 - 5] 도 가능).
따라서 DFS를 재귀로 수행하면서 재귀호출이 끝나는 시점의 노드를 stack에 담아 역순 처리하기만 하면 된다.
역방향 간선이 있는 경우, 즉 사이클이 있는 경우, 이를 감지해낼 수도 있다.
DFS방문 시 기본적으로 활용하는 visit이라는 배열 외에,
추가 배열을 하나 선언(temp라 하자)하여 재귀호출이 끝나는 시점(스택에 노드를 담는 시점)에 해당 노드를 표시한다.
만약 탐색 도중, temp에 표시되지는 않았는데(아직 탐색중인 route인데) visit에는 표시되어있다면,
그 노드는 현재 탐색중인 route 위에 놓여져 있는 노드임에도 이미 방문한 노드라는 의미가 되고,
이는 즉 그래프에 사이클이 존재한다는 의미이다.
3. 위상정렬 방법 2 - BFS
각 노드의 입력차수(indegree)를 지워나가면서 큐로 구현하는 방법이다.
왜 굳이 입력차수를 지워나가야 할까?
아래 그림을 보면,
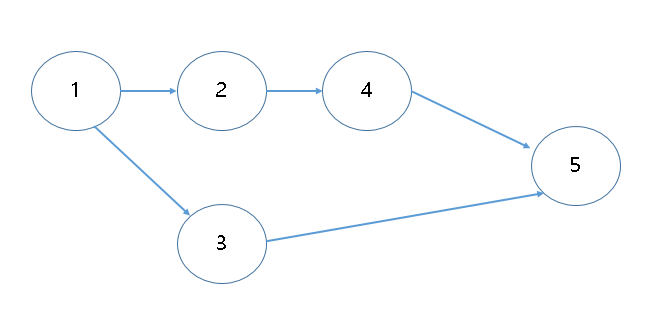
위상정렬의 결과는 1 - 2 - 3 - 4 - 5 또는 1 - 3 - 2 - 4 - 5 가 되어야 한다.
만약 일반적인 BFS를 1번 노드를 정점으로 하여 시행한다면,
1에 연결되어있는 두 노드 2,3 중 3이 큐에 먼저 push 될 가능성이 있고,
이 경우의 답은 1 - 3 - 5 - 2 - 4 가 되어 위상정렬이 되지 않는다.
indegree가 없는 노드란 정점 노드에서 이어지는 다음 순서의 정점 노드를 의미하므로,
큐에 노드를 넣을 때 정점 노드에서 간선을 제거한 이후에 indegree가 없는 노드부터 넣어가면
위상정렬이 완성된다.
따라서,
1) 각 노드의 indegree를 세고 배열에 담는다.
2) 동시에 indegree가 없는 정점(1개 이상이 될 수 있음)을 큐에 담는다.
3) 큐에서 노드를 꺼낸 후(정점), 해당 정점 노드와 이어진 간선을 제거한다 -> 1)번의 배열에서 정점 노드로부터 indegree를 받는 노드의 간선 개수를 빼준다.
4) 꺼낸 노드의 노드 번호를 기록한다.
5) 위 과정을 노드 수 n번만큼 반복한다.
그런데 위 과정을 n번 반복하는 중 큐가 empty 상태가 된다면?
이는 그래프가 Acyclic 이 아니라 Cyclic Graph 라는 것을 의미한다.
-> 반대로 말하면, 이 방법을 통해 해당 그래프에 사이클이 있는지 검증할 수 있다.
(즉, 사이클이 있다면 해당 그래프는 DAG가 아니다)
아래 그림을 보자.
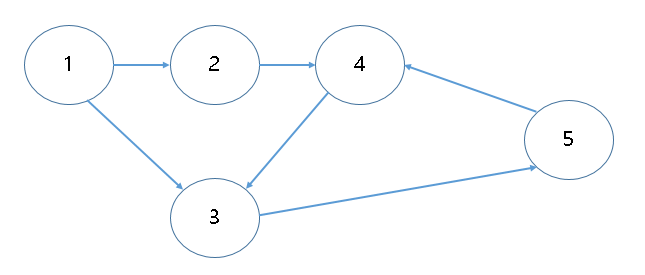
4 - 3 - 5 에 사이클이 존재한다.
위 방법을 이용한다면,
1) 큐에 1이 담긴다 -> 1의 간선을 제거한다.
2) 큐에 2가 담긴다 : 3은 4에서 나온 indegree가 있으므로 담을 수 없음
3) 2를 꺼내서 2의 간선을 제거한다 : 4에 5에서 나온 indegree가 있으므로 담을 수 없음.
큐에 더 이상 담을 노드가 없으므로, empty에서 종료되고, 수행 횟수가 노드 개수보다 적으므로 해당 그래프는 DAG가 아님 -> 위상정렬을 수행할 수 없음.